3 февраля 2019 года

Уважаемые коллеги!

Многим участникам проекта «Зимняя ПсихоМетрическая Школа» (и тем более тем, кто в этом проекте не участвует) осталось не вполне понятным, почему я такой акцент сделал на… четырехклеточных таблицах сопряженности (ЧТС).

А ведь дело всего-навсего в том, что ЧТС — это инструмент, необходимый для развития самого ценного, что должно быть на вооружении у диагноста-оценщика — ЭТО ВЕРОЯТНОСТНО-ЛОГИЧЕСКОЕ МЫШЛЕНИЕ.

Приведем здесь такую юмористическую задачку (которую я еще не использовал в материалах ЗПМШ, так как наткнулся на эту шутку в ФБ только вчера). Я постарался встроить шутку в контекст применения ЧТС для … вероятностно-диагностического вывода о том, как связан диагностический признак и диагностическая категория.

ПСИХОЛОГИЧЕСКИЙ ПРАКТИКУМ НЕ ТОЛЬКО ДЛЯ… МУЖИКОВ.

Уважаемые участники группы TESTbyTEST.

Вот Вам очередная задачка в духе ПсихоЛогического практикума.

Какой логический вывод напрашивается из суждения «Не ходил за покупками с листочком — не мужик»?

а) Все, кто ходил с листочком, — мужики.
б) Некоторые, кто ходил с листочком, — мужики.
в) Отсутствие листочка дает возможность сделать какой-то вывод, а наличие листочка НЕ дает.

Итак, применим для анализа этой ситуации и обоснованного диагностического вывода, аппарат ЧТС. В данном случае:

«Наличие листочка (или списка покупок в мобильном)» — это диагностический признак.
«Вывод о гендерной принадлежности носителя листочка» — это диагностическая категория.

Обе переменные — это простейшие качественные бинарные переменные, которые могут принимать лишь два значения каждая. Признак может быть такой: «ходил с листочком — не ходил с листочком».

А диагностическая категория может быть такая: «мужик — не мужик».
Мы вполне можем назвать каждую переменную логической, ибо что такое логическая переменная? — Это переменная с двумя значениями — «Истина — Ложь». По сути любую качественную, бинарную переменную можно рассматривать как логическую переменную.

Теперь построим ЧТС следующего вида:

	Мужик	Не мужик
Ходил с листочком	A= ?	B= ?
Не ходил	C=0	D=100%

Что нам известно из афористического суждения, с которого мы начали: «Не ходил — не мужик». Примем условно (временно) это суждение за истинное и достоверное знание. Тогда … нам известны значения эмпирических вероятностей в нижней строчке ЧТС. Что нам известно для заполнения клеточек таблицы? — Нам известно, что надо проставить в нижней строке! Известно, что вероятность события D равна 100 процентам (будем использовать эту наиболее понятную для гуманитариев единицу измерения вероятности, а не в пугающих дробных десятичных долях от единицы). При этом значение в клеточке С автоматически равно 0 процентов. Ну а теперь зададимся вопросом, а что нам известно про первую строчку таблицы? — А ведь, строго говоря, ничего не известно. Поэтому правильное решение этой задачи — ответ «в» (а не ответы «а» и «б»; пояснение: буква «а» в этом контексте это не клеточка таблицы, а первый ответ в тестовом вопросе). Дело в том, что мы не знаем, должно ли при этом значение в клеточки А быть равным 100% (ответ «а») или только 50% (ответ «б»). У нас есть неопределенность: мы не знаем, в каком интервале находятся эти значения (!). И логически мы НЕ можем вывести из значений во второй строке состояние клеточек в первой строке.

Как должна была бы выглядеть таблица, если бы был верен ответ «а» ? — Очевидно следующим образом:

	Мужик	Не мужик
Ходил с листочком	А = 100%	B = 0%
Не ходил	C = 0%	D = 100%

Что за тип отношения отображен в этой второй таблице? — Правильно, это отношение эквивалентности двух множеств событий (двух логических переменных), или так называемое взаимно-однозначное соответствие. Но.. нет оснований делать вывод о том, что ЧТС имеет точно такой вид и что А = 100%. Может быть это так, а может быть и не так! — Мы НЕ знаем. Как узнать? — Надо изучать обязательно не только людей, которые НЕ ходили с листочком, а надо изучать и «контрольную группу» — тех, кто ходил (хотя чаще группу в первой строке мы называем «экспериментальной»). Вполне возможно, что среди «ходивших» есть «не мужики», тогда первая строка таблицы НЕ дает нам никаких оснований делать какие-либо определенные прогнозы (выставлять диагнозы). Из состояния второй строки состояние первой НИКАК ЛОГИЧЕСКИ НЕ ВЫТЕКАЕТ (!). — Вот это очень важный вывод из этого смешного элементарного анализа.

Это вывод имеет большое значение, так как на уровне обыденного сознания люди очень часто приравнивают (действуя не осознанно, то есть автоматически) неправомерным образом отношения импликации (включенности) и отношения эквивалентности. Из одной строки таблицы у них автоматически возникает в голове определенное заполнение клеточек другой строки (!). Поэтому они и выбирают очень часто ответ «а», не отдавая себе даже сознательного отчета, что случилось, то есть делают вывод: «Листочек — есть признак мужественности-женственности» (комизм этого признака помогает нам понять, что это вовсе не так).

Откуда берется эта ошибка обыденной логики (по сравнению с научной)? — ЕЕ происхождение связано с тем, как устроены наши… нейронные сети. Дело в том, что они накапливают статистические связи между событиями и … делают вывод о наличии корреляции между бинарными признаками, когда имеется только часть наблюдений (за второй строкой таблицы). Возникает ошибочное связывание (корреляция): Из факта «нет листочка — не мужик» вытекает «листочек — это диагностический признак, скоррелированный с категориальным событием МУЖИК».

Прошу задавать здесь вопросы, чтобы мы ВМЕСТЕ довели этот пример до полной прозрачности.

Пока я продолжаю и продолжаю повторять, что обыденная логика является некорректной — не является носителем вероятно-логического мышления. Ибо она генерализует (распространяет) информацию, которая вытекает из односторонней связи (исследованной и выявленной на одной выборке людей) на всю четыре случая — на всех людей. Чтобы не делать этого чрезмерного и неадекватного обобщения, надо научиться постоянно анализировать не 2, а четыре случая. Надо понять, что все эти четыре случая — это РАЗНЫЕ случаи. А это означает, что надо привыкнуть ориентироваться в четырехклеточных таблицах.

Завоеванная Н.С.:

За мужиков обидно, Александр Георгиевич.

Можно еще такую сделать:

	Женщина	Не женщина
Посылала мужика	A= 50%	B=50%
Не посылала	C=0	D=100%

Ммм…и листочек совсем не обязателен

Получается информативная строчка только нижняя, а С растворяется в D. Импликативные отношения двух множеств. Надеюсь, я правильно помню лекцию.

Шмелев А.Г.

«Посылала мужика»? — Спасибо, Наташа, за очень веселую формулировку.
Конечно, мужика может послать не только женщина, но и… другой мужик.
Даже неодушевленное устройство вроде «электронного табло» тоже может
«послать мужика»… 

Благодарю Вас за результативную попытку творческого освоения метода ЧТС!

Ваш АШ

А теперь попробуем смоделировать логико-вероятностные отношения в рамках ЧТС с помощью простейших нейросетевых моделей (используется при этом простейшее модельное представление о нейронах, которые есть ничто иное как вершины (узлы) в дискретном математическом графе, которые могут находиться в каком-то промежуточном состоянии в интервале от 0 до 1, где 0 — заторможен, а 1 — возбужден).

При этом покажем, что такое «Третья сигнальная система» в самом элементарном ее фрагменте, обеспечивающим логическое различение отношений эквивалентности-корреляции и отношений импликации (односторонняя вероятностная зависимость бинарных событий).

На рис 1а. мы видим модель, всем хорошо знакомую из базового курса обучения элементарным представлениям в рамках физиологии ВНД (классические условные рефлексы по Павлову) и теории поведения (классический бихевиоризм по Уотсону-Торндайку)): чем сильней условная связь P, которая связывает два события S (стимул-сигнал) и R (реакция), тем с большей вероятностью при появлении стимула S возникает реакция R.

Во второй сигнальной системе нет ничего принципиально отличающегося от первой сигнальной по сложности в связях между S и R, просто на месте S могут оказаться «слова» (речевые команды). Как происходит дрессура: положительное подкрепление связи между S и R — нейронами, которые между собой изначально не связаны (P=0), приводит к появлению условной связи (P > 0 и постепенно приближается к 1).

Что означает классический (павловский) условный рефлекс? — Это корреляция двух событий в мозгу собаки: S «Звенит звонок» — R «Выделяется слюна (потому что ожидается корм)». Угасание условной связи — это падение силы связи через промежуточный нейрон P (впрочем, можно электро-физиологически интерпретировать это и по-другому — как повышения сопротивления в аксоне-проводе S-R, что затормаживает движение нервного импульса по волокну между S и R). Но пока этого угасания не произошло отсутствие звонка не приводит к выделению слюны, так как высокие значения P автоматически означают, что значений Q=1-P стремится к нулю. Я уж не стал рисовать на рисунке 1а вторую промежуточную клеточку Q, чтобы не усложнять эту картинку. Но Q в простейшей нейросети есть просто прямая альтернативная связь по отношению к клеточке P, так что Q = 1 — P (клеточки P и Q связаны простейшими реципрокными отношениями взаимного торможения). Когда появляется в нашем сознании слово «листочек», то возникает ответная ассоциативная реакция «мужик» (работает связь P), а когда появляется сообщение «нет листочка», то срабатывает связка Q (обратная P) и появляется автоматический вывод «не мужик».

Несколько более сложная, но более забавная история, связана с с оперантным (скиннеровским) условным рефлексом. Он ведь тоже может формироваться во Второй Сигнальной системе, то есть в простейшей нейросети с одной-двумя промежуточными связующими клеточками. Вспоминается анекдот про психолога-бихевиориста, который отучил детей играть в свистульки под его окном: 1) Вначале он стал дарить детям монетки, чтобы больше свистели. 2) На втором этапе прекратил оплачивать эту «работу». 3) Дети заявили, что «бесплатно работать не будут». Величина P банальным образом зависит от подкрепления («монетки»). Убираем подкрепление и величина P сразу резко снижается (P стремится к нулю), так что вероятность реакции R (реакции на место «под окном профессора») резко падает.

В мозгу детей связь между «свистульками» и «удовольствием от свиста» погасла, когда сформировалась связь между «свистульками» и «монетками». Мозг детей функционирует по принципам Второй Сигнальной Системы, но не по принципам Третьей (поэтому дети проигрывают в рефлексивной игре с профессором).

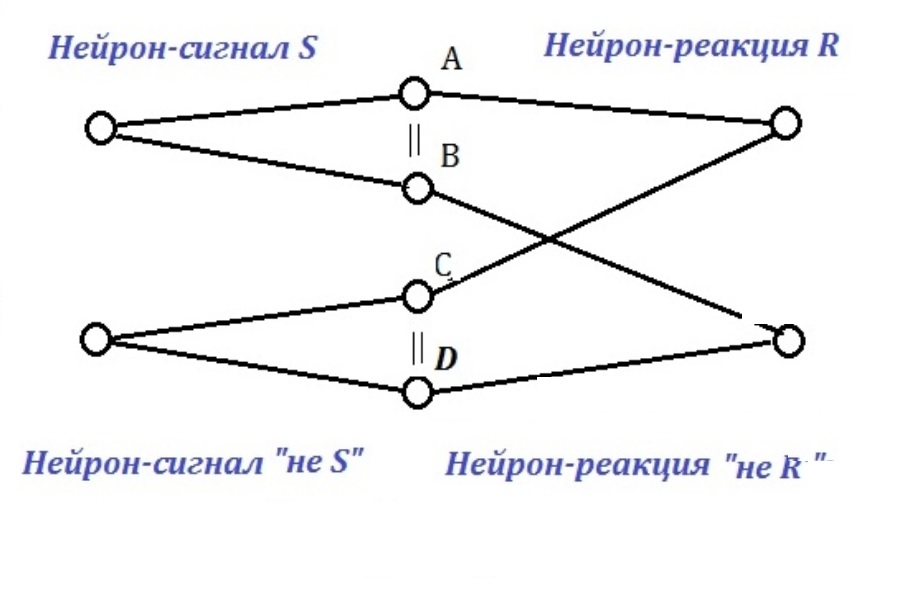
А вот в «третьей сигнальной системе» все сложнее и это обеспечивает независимость между клеточками P и Q. Вместо клеточки P начинает работать пара промежуточных клеточек A и В, а вместо клеточки Q — пара клеточек C и D. Внутри двух пар A-B и C-D есть реципрокные отношения (так что B= 1 — A и D = 1 — C), но между элементами разных пар таких связей НЕТ. Поэтому в такое случае информация «нет листочка» не ведет к выводу «не мужик».