Итак, коллеги, вашему вниманию здесь предлагается вовсе не полноценная и продуманная статья, а лишь незавершенный набросок. Тема возникла спонтанно — в ходе разговора в чате моего ТГ-канала «Компьютерная психодиагностика и психосемантика». Я вспомнил, что за 40 лет преподавания отдельных весьма и весьма легких разделов прикладной статистики в МГУ натыкался каждый год на удивительные случаи глубокого непонимания самых простых математических терминов и объектов (таких как графики, таблицы и даже обыкновенные дроби). Я начал было попытку группировки этих моих впечатлений и пронумеровал последовательно 3 несколько отличающихся «синдрома». Моя сквозная мысль состоит в том, что в большинстве случаев я сталкивался не столько с особенностями когнитивного стиля (с некоторым «гуманитарным складом ума»), а с банальной выученной беспомощностью в области сАмой элементарной математики.

Как-то я не увидел всплеска интереса к этой теме в ТГ-чате. Но допускаю, что тема все-таки интересная, а отсутствие реакции в ТГ-чате скорее является свидетельством того, что там у меня мало подписчиков, а те, кто подписался, не особенно интересуются этой темой. Поэтому делаю попытку опубликовать незаконченный список из трех синдромов для более широкой аудитории — для читателей «блога А.Г.Шмелева».

Вспоминается, что когда-то тема, связанная с трудностями усвоения математики студентами-психологами, была едва ли не самой популярной среди моих публикаций в Рунете — на нее было больше всего откликов (причем самых разных). Но это было еще в те добрые старые времена (начало века), когда Яндекс еще позволял увидеть популярность тех или иных публикаций — количество перепечаток на разных сайтах, количество комментариев и так далее. Теперь, когда Яндекс коммерциализировался, все это увидеть и сравнить очень и очень непросто (на глаза попадаются те, кто за это смог заплатить — за то, чтобы попасться на глаза).

========================

Итак, список операциональных признаков «выученной беспомощности в работе с математикой» (которая называется нередко с помощью весьма учтивого выражения «гуманитарный склад ума»).

1) Страх перед формальными (буквенными) обозначениями переменных и понятий. Пример: если сформулировать задачу так: «Саша имел 2 яблока, а Коля — три», то страх не возникает. А если задачка сформулирована так: «Субъект A имеет X яблок, а субъект B имеет Y яблок», то возникает страх, который блокирует сам процесс осмысления задачи и поиск даже самой элементарной операции. А уж формализованного ответа типа «Всего яблок у двоих X+Y» вообще можно не дождаться никогда.

Причина: не было достаточного тренинга, помогающего демистифицировать переход от конкретных цифр к буквам и обратно. Буквы всегда предъявлялись в более сложных задачках, а надо было начинать с более простых — как в указанном примере.

2) Привязка к конкретным образам и частным случаям. Например, если прямоугольный треугольник изобразить так, что основанием становится гипотенуза, а не один из катетов,  то такой прямоугольный треугольник уже «не выглядит» прямоугольным. Эта же негибкость и неуниверсальность геометрических моделей для абстрактных понятий проявляется и в неспособности выполнить банальную операцию транспонирования таблиц: если поменять строки и столбцы местами, то человеку кажется, что это уже ДРУГАЯ ТАБЛИЦА, хотя изменилась  только пространственная ориентация строк и столбцов, а смысл не поменялся никак. Люди с такими дефектами в навыках, например, не могут разглядеть идентичность двух четырехклеточных таблиц сопряженности:

Что же  является причиной такой негибкости и конкретности образов? — Отсутствие практики «умственного вращения», а в более общем случае — умственного манипулирования образами с целью отделения инвариантных преобразований (не меняющих структуру образа, а затрагивающих только его ориентацию в пространстве) от структурных изменений. По моим наблюдениям такие люди в детстве никогда не играли в конструкторы, не пользовались вспомогательными картами в книгах (хотя бы изображающими, где находится домик Винни-Пуха по отношению к домику Пятачка). В тяжелых случаях такая негибкость образов выражается, например, в топографическом кретинизме.

При этом у человека с такими  почти болезненными дефектами мышления может присутствовать ОГРОМНЫЙ запас слов. Он может успешно изучать даже несколько иностранных языков (!), но не сможет найти дорогу домой, если в городе окажется в трех кварталах от своего дома. Почему? — Нет никакого мысленного «вида сверху» на план города. 

Новейшие исследования (см. диссертацию Никиты Хохлова, в частности) показывает, что ядром математических способностей является не столько работа с символами (сама по себе) или работа с геометрическими образами (сама по себе), сколько способность устанавливать гибкую связь между тем и другим — между символами (абстрактными понятиями) и образами. Таким образом, речь идет не о пространственном мышлении самом по себе, а о скоординированности пространственного и вербального мышления.

Когда используется модный термин «клиповое мышление», то во многом под этим подразумевается как раз «привязка к конкретным образам».

Продолжаем список (и на этом третьем пункте я, пожалуй, остановлюсь, ибо интерес к этому списку проявляют…гм… одни и те же люди, а круг их вовсе не расширяется).

3) Непонимание дробей и относительных величин. Когда я допытывался, как студент МГУ еще в школе превратился в «математического инвалида», то я не раз сталкивался с таким сенсационным парадоксом: люди, которые не могут проинтерпретировать банальный коэффициент четырехклеточного сопряженности типа КД (коэффициент дискриминативности) на самом деле не владеют устойчиво даже различением … числителя и знаменателя в обыкновенных дробях !!

Ну, ребята, если Вы Не можете даже это превратить в актив, а не в пассив собственного мышления, то на что можно надеяться в деле  усвоения статистики, да и не только статистики, а, например,… экономики. Ведь любой расчет эффективности должен содержать в знаменателе расходы. Но наши «гуманитарии» скорее умеют складывать и вычитать, чем делить и умножать (то есть работать умеют только с аддитивными шкалами, но не с мультипликативными!). Поэтому они могут подсчитать только абсолютную сумму прибыли ПРИХОД — РАСХОД, но не могут посчитать… банальнейший коэффициент рентабельности ПРИХОД/РАСХОД, который необходим для сравнения эффективности разных бизнес-планов и реальной эффективности разномасштабных компаний (или разных секторов деятельности внутри одной компании). Грубо говоря, они не могут сказать, что компания B работает более эффективно, чем компания А, хотя у нее меньше приход.

Эффективность компании А = Приход/Расход = 2 млн / 1,5 млн

Эффективность компании B = Приход/Расход = 400 тысяч / 120 тысяч

Мне недавно пришлось объяснять БУХГАЛТЕРУ своего ТСН (товарищества собственников жилья), что нельзя без ущемления интересов владельцев маленьких участков (к каким отношусь я сам), если всем владельцам добавлять одну и туже сумму повышения коммунальных платежей в виде СЛАГАЕМОГО, а нужно умножать на общий для всех коэффициент повышения (раз до этого учитывался в сумме платежей размер участка). Но бухгалтер… отказывалась понимать (глагол в женском роде, так как это женщина), что формулы справедливости базируются на относительных величинах и мультипликативной шкале (см. теорию справедливости Джона Ролза), так как у нее — лично у этого буха — в голове… аддитивная шкала (!!).

И это у нас не один такой бух в стране России, а таких «гуманитариев» у нас МИЛЛИОНЫ (!). Их даже счетоводами трудно назвать, а не то что людьми с «экономическим мышлением». Это «математические инвалиды». И другого слова тут не подберешь. Доля фактических баллов «неуд» в нашей стране превышает за ЕГЭ по математике фактически 50%, только Вы никогда не услышите этой цифры, ибо это… государственная тайна.

Все это приводит к непониманию многими студентами-психологами того, как работают ЧТС — четырехклеточные таблицы сопряженности для расчета валидности отдельных тестовых заданий и тестов в целом. Ибо … даже с дробями не научились работать (!).

Кстати, неумение работать с дробями приводит, в частности, и к непониманию того, что процентные величины целиком зависят в своей интерпретации от того, какая именно величина принимается за 100 процентов, то есть оказывается в знаменателе дроби. Люди готовы услышать «экзамен сдан на 95%», но не задаются вопросом, а какая величина берется при этом за 100%, что именно стоит в знаменателе (!). Поэтому они всегда путают шкалу ППО (когда в знаменателе максимально возможное число правильных ответов) и шкалу процентилей (когда в знаменателе общее число участников тестирования).

Кстати, мы пытаемся исправлять такие дефекты математического мышления на нашей «дистанционной психометрической школе». Иногда удается! — Я не могу сказать, что удается всегда (это было бы нечестно), но меня всегда удивляет в этом случае позитивный результат: в короткий срок некоторые пытливые люди вдруг начинают работать с простейшими дробями вида:

Трудность задания в процентах = 100% — 100 * ( ЧПО / N ),

где ЧПО — число правильно ответивших, а N — общее число ответивших на это задание.

Завершаю незавершенный перечень синдромов ссылкой на страницу про наши дистанционные обучающие программы на сайте ht-line.ru:

Дистанционная психометрическая школа (курсы)

На обложке Гигачат изобразил человека по моему запросу «Изобразите математического инвалида — такого человека, который забыл таблицу умножения и путает числитель и знаменатель в дробях».

Надо сказать, что это результат второй попытки. Вначале Гигачат совсем не справился с задачей и изобразил довольно-таки умного, даже симпатичного паренька, на столе у которого куча книг (см. предпоследний рисунок в статье). Но… после второй попытки, когда я его укорил за книги на столе, этот наш Гига-умник убрал книги со стола, а глаза сделал более узко посаженными и сведенными к переносице, ну типа «силится парень что-то понять, но не может никак…»

А на последнем рисунке мы видим совсем уж неполиткорректную карикатурку из галереи «Яндекс-картинки». Это в ответ на тот же самый мой запрос к Алисе: «Найди изображение математического инвалида». Почему не политкорректная эта картинка? — Откровенный сексизм, как будто все опять сводится к анекдотам «про блондинок». В общем как было плоховато у нейронок наших с ЧЮ, так и осталось…

P.S.1.

Сегодня я почитал эту вчерашнюю мою статью и подумал, что некоторым читателям будет не хватать ясного определения понятия «выученная беспомощность». Я обратился за помощью к Яндекс-Алисе. Цитирую ниже ответ:

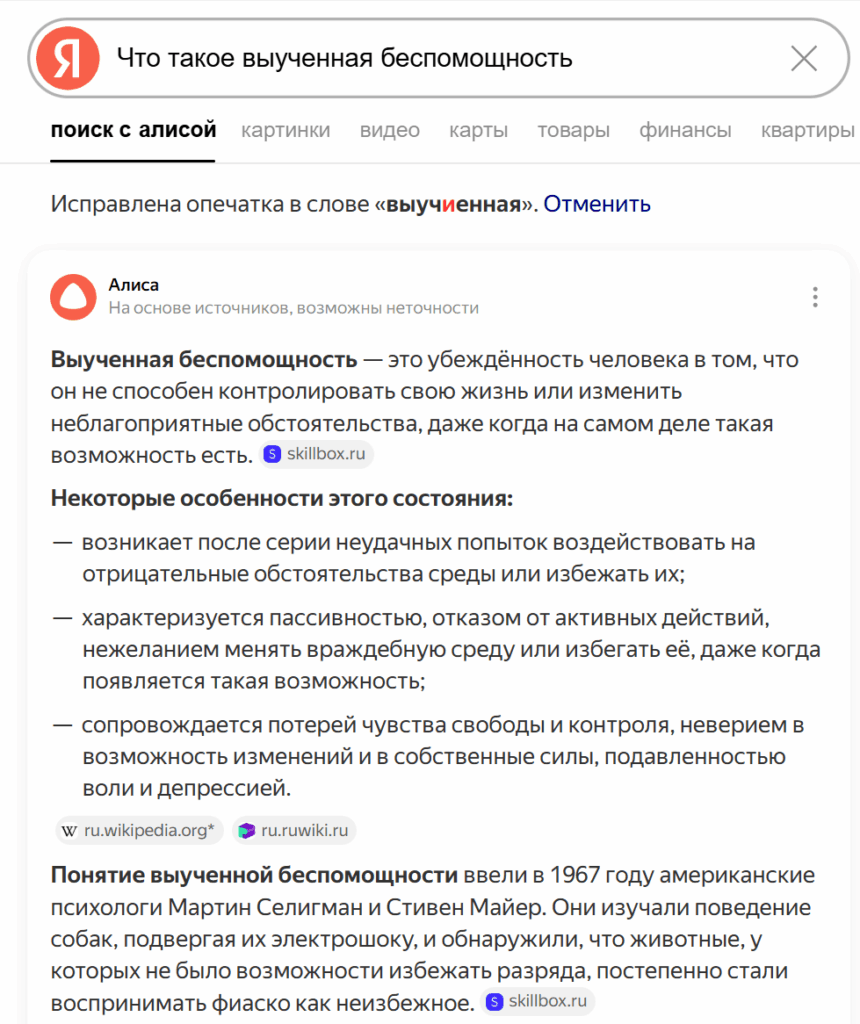
P.S.2.

Я решил начать коллекционировать примеры выученной беспомощности в области математики — примеры вопиющих ошибок. Пока у меня описаны только три случая. Но уже сегодня я наткнулся, пожалуй, на четвертый:

https://sponsr.ru/ashmanov/43738/Znakomstvo_O_chem_blog

Игорь Ашманов, которого я здесь цитирую, назвал свой блог «Что по осям» скорее метафорически, но я его пример беру в свою коллекцию в буквальном смысле. Ведь очень часто не только школьники и студенты, но и очень серьезные докладчики (даже на защитах диссертаций я это наблюдал не раз) не могут не только подписать оси на своих же графиках, но и внятно ответить на вопрос, а что у них по осям (!).