Итак, дорогие мои, мы начали всерьез готовиться к нашей дистанционной зимней психометрической школе (ЗПМШ-26). А это значит, что надо еще и еще раз подумать мне о том, как сделать наш подход более прозрачным и НАГЛЯДНЫМ для тех, кто с трудом осваивает базовые психометрические понятия «надежность» и «валидность». К сожалению, разговор про трудность усвоения в данном случае — это не выдумка с нашей стороны, а «медицинский факт», ведь часть наших слушателей каждый год изрядно мучается с осмыслением этих понятий…

Казалось бы, ну что может быть проще «четырехклеточных таблиц сопряженности» (сокращенно ЧТС)? Я многие годы думал, что уж в этом-то случае умственное представление о корреляции двух бинарных переменных ухватить совсем-совсем просто. Ведь всего с четырьмя клеточками мы имеем дело — A-B-C-D (!). Но … так обстояло дело, когда я работал со студентами МГУ. Хотя бывало среди студентов-психологов и немало лиц с так называемым «гуманитарным мышлением», но все-таки большинство справлялось с построением и анализом таблиц ЧТС без особого труда.

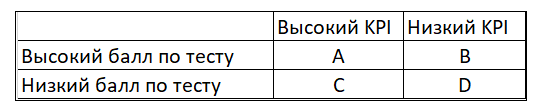
Таблица 1. Принципиальная схема ЧТС для проверки валидности теста.

Но… Другое дело — это люди более старшего возраста, уже поработавшие на производстве в должности эйчаров-оценщиков и желающие (искренне желающие!) повысить свою квалификацию! Вот тут свежести математического абстрактного мышления нередко не хватает.

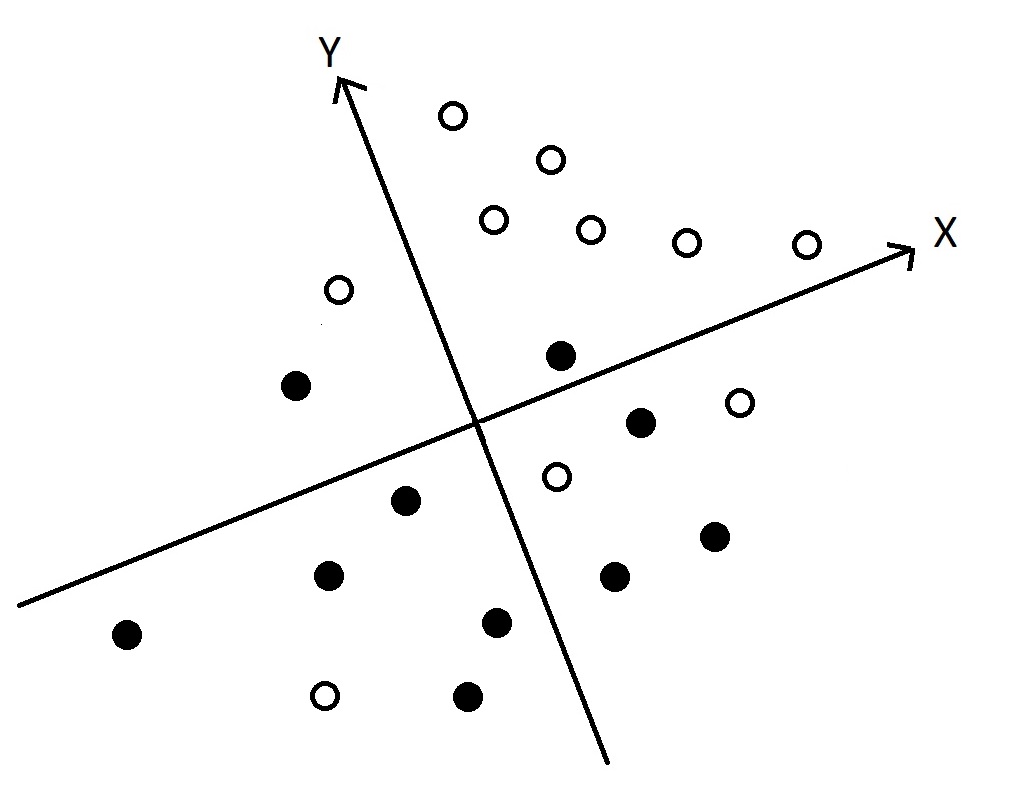
И вот что я придумал, друзья, в этом году. А придумал я предложить для осмысления ЧТС такой вспомогательный «наглядный пример», или «образную метафору» (называйте, как хотите). Представьте себе вид сверху — с балкона — на школьный дворик. На нем толпятся девочки в белых чепчиках и мальчики в черных кепочках. Изобразим белые и черные головные уборы детей с помощью белых и черных кружков на плоскости (как это схематически показано на рисунке, вынесенном мной на обложку этой статьи). Дети стоят немножко вперемешку, но все-таки большинство девочек тяготеют ближе к девочкам, а большинство мальчиков — соответственно ближе к мальчикам. А теперь представьте себе, что перед нами возникла задача, не перемещая детей, провести по двору натянутую ленточку так, чтобы как можно больше девочек оказалось с одной стороны и как можно больше мальчиков — с другой. Иными словами, ленточка у нас будет выполнять роль «разделяющего теста», направленного на то, чтобы разделить (дифференцировать, дискриминировать) девочек и мальчиков.

Вы тут можете спросить: «А зачем разделять мальчиков и девочек? И что это за глупый тест такой?». Ну тогда давайте предположим, что мальчики и девочки выполняли у нас два теста: тест X — это тест по истории, а тест Y — это тест по русскому языку. Ну и так получилось, что девочки выполнили оба теста лучше, чем мальчики: большинство девочек и по тесту X, и по тесту Y показали результат выше среднего, а большинство мальчиков — ниже среднего (хотя и в том, и в другом случае были исключения). Вот теперь у нас возникает ситуация близкая к такой, которую мы имеем при проверке валидности тестов, но только «девочки» — это у нас «высокая группа» (работники с высоким KPI), а мальчики — это «низкая группа» (работники с низким KPI). Иными словами: белые кружки обозначают местоположение работников из высокой группы (в пространстве результатов по двум тестам X и Y), а черные кружки — местоположение работников из низкой группы.

Главное, что теперь нам надо удерживать в памяти (в рамках нашей умственной геометрической модели), — это то, что изображающие точки в пространстве — это ЛЮДИ (люди-люди-люди! — если повторить много-много раз, то иногда доходит). А вид сверху на школьный дворик (ну пусть с вертолета, чтобы совсем сверху было) — это наглядная (графическая) метафора для понимания того, что такое пространство результатов (оно же — «корреляционное поле»).

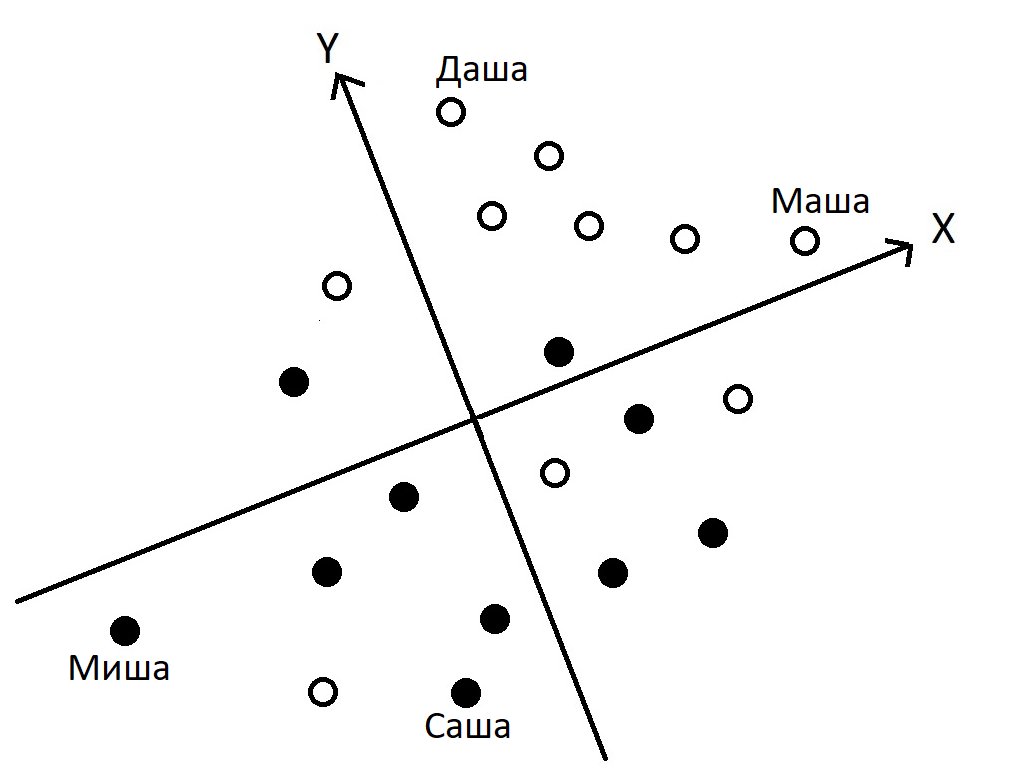
Рисунок 1. Изображение людей в пространстве значений по двум тестовым переменным X и Y.

Но давайте не будем рисковать и для еще пущей наглядности все-таки подпишем хотя бы четыре изображающие точки именами, как это показано на рисунке 1. Чем примечательны Даша и Маша? — У Даши самый высокий результат по русскому языку (ортогональная проекция на ось Y дает самый высокий результат именно для точки по имени «»Даша»). А у Маши самый высокий результат по истории (самое высокое значение по оси X). Соответственно у Саши самый низкий результат по русскому, а у Миши — по истории. Видно это вам на рисунке 1, да? — Ну если видно, то я очень рад этому! Поехали дальше…

Теперь давайте построим ЧТС для истории X и для русского Y. Впрочем, я сделал это и изобразил эти самые ЧТС прямо на рисунке 2 — в соответствующих координатных углах.

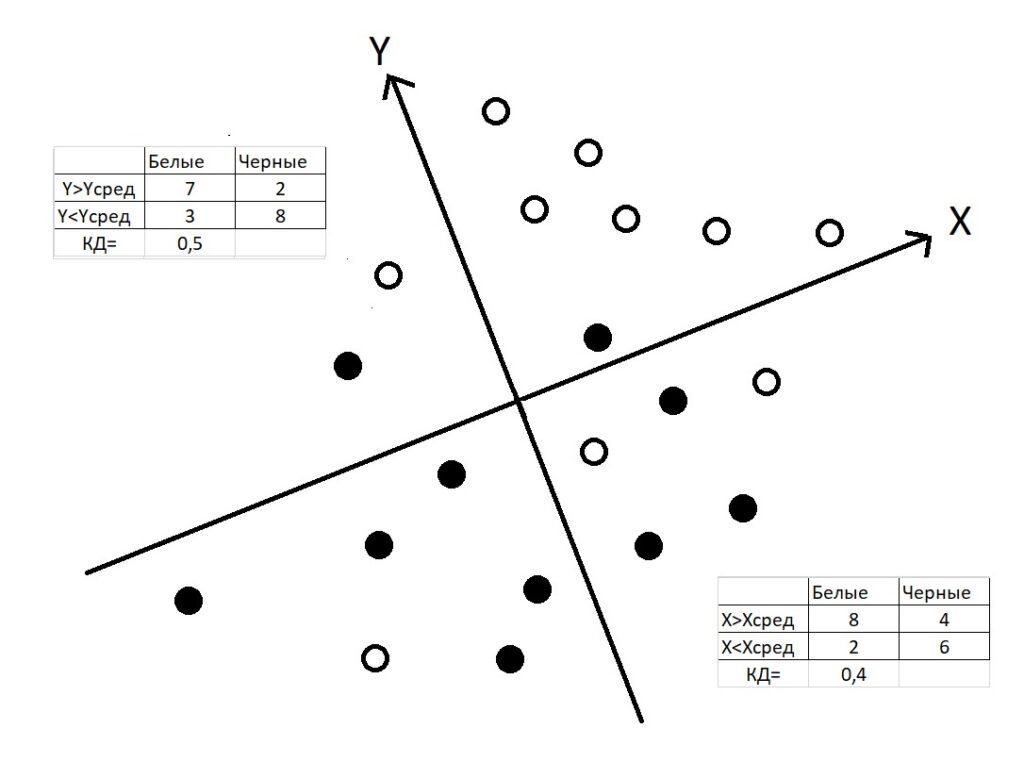
Рисунок 2. ЧТС для бинарной переменной X (тест по истории) и бинарной переменной Y (тест по русскому).

Давайте сверим с Вами, как мы получаем значения в клеточках ЧТС. Левая верхняя клетка (ее обычно обозначают буквой А) содержит в ЧТС по русскому значение 7. Что это означает? — Это означает, что 7 белых кружков получают положительные проекции на ось X — баллы по русскому выше среднего Xсред. Как Вам самостоятельно подсчитать число белых кружков для верхней левой клетки? — Надо просуммировать число белых кружков выше оси X (именно такие кружки, получают положительные значения по оси Y). У Вас получилось теперь число 7? — Если получилось, отлично! — Поехали дальше…

Теперь поймем, откуда же берется число 3 в левой нижней клетке в ЧТС по русскому? — Вы, наверное, теперь сами смогли догадаться, что надо просто подсчитать число белых кружков ниже оси X и получить это самое число 3. Ровно столько девочек (или работников из эффективной группы в нашей фирме) все-таки справились хуже среднего по русскому.

Теперь Вам понятно, почему в правой верхней клетке ЧТС по русскому стоит число 2? — Это ведь число черных кружков выше оси X. Это означает, что только 2 мальчика (работника из малоэффективной группы) смогли показать баллы выше среднего по русскому языку. Вот они и попали в клетку B! Что такое клетка B? — Это число людей, получивших такое сочетание двух бинарных переменных, когда человек принадлежит к «высокой группе по тесту» (балл по русскому выше среднего), но к «низкой группе по производительности труда» (черная шапочка). Ну теперь уж Вас не составит труда подсчитать число «черных шапочек» ниже оси X. Впрочем, их можно и не считать, ибо я для простоты уравнял число белых и черных шапочек на нашем «корреляционном поле» — их всего по 10 штук. Поэтому 10-2 = 8, вот столько у нас мальчиков оказались с баллом ниже среднего по тесту «русский язык».

А ТЕПЕРЬ ПРО ТЕСТЫ ОТБОРА И ОТСЕВА

Говорят, чтобы осмыслить, что такое тесты отбора и отсева и чем они отличаются друг от друга, надо рисовать два горба на распределении тестовых баллов. И я это тоже много лет делал. Но давайте не будем выходить за пределы ЧТС, раз уж мы освоили этот самый простой схематизм. Уже в ЧТС можно увидеть, чем различаются тесты отбора и тесты отсева.

Кого лучше разделяет тест по русскому языку — мальчиков или девочек? Видим, что контраст выше для второго столбца (для черных шапочек), чем для первого. В верхнюю группу попадают 7 из 10 девочек, а в нижнюю группу — 8 из 10 мальчиков. То есть, данный тест по русскому языку лучше разделяет «черные шапочки» , то есть мальчиков, чем «белые шапочки». Можно сказать «разделяет», а можно сказать «выделяет» (диагностирует). Но вспомним-ка еще раз, кто такие условные «мальчики» в нашем примере? — Это работники из малоэффективной группы. А значит, наш тест по русскому лучше диагностирует слабых работников! То есть, он лучше работает как тест отсева, а не как тест отбора! Его эффективность в случае отсева составляет 80%, а в случае отбора — только 70%. Это теперь понятно? Это видно на числовых значениях в левой верхней четырехклеточной таблице?

Справка немного в сторону. В логике так называемой «матрицы ошибок» (confusion matrix, что есть просто другое название ЧТС) тест отсева имеет более низкую вероятность ошибки типа «пропуск», но более высокую вероятность ошибки типа «ложная тревога». В доказательной медицине в этом случае говорят, про асимметрию в показателях «чувствительность» и «специфичность» (но всеми этими понятиями весьма непросто овладеть при чтении одной этой статьи, надо бы позаниматься с ними практически в рамках школы).

Аналогично правая нижняя таблица показывает нам, что тест по истории, напротив, лучше работает как тест отбора. Его эффективность при разделении «высокой группы» (белых шапочек) достигает 80%, а при разделении низкой группы — только 60% (в правую нижнюю клеточку D в этой ЧТС попадают только 6 черных шапочек).

А когда нам приходится выбирать между тестами отбора и отсева? — В ситуации, когда мы можем реально успеть предъявить испытуемым (соискателям на должность) не два, а только один тест. Конечно, если есть возможность проводить сразу 2 теста, то тогда и отбор, и отсев работали бы одинаково хорошо. Но … нередко такой возможности просто нет даже… по банальным финансовым причинам. Например, предположим, что и тест по русскому , и тест по истории — это профессиональные инструменты, которые разработаны сторонней организацией и надо платить за лицензию на каждый запуск каждого теста. Тогда…гм… приходится экономить и выбирать один из двух тестов, так ведь? Какой же и в каких случаях выбрать? — Ответ: в ситуации избытка кадров нам полезней использовать тест отсева по «русскому» (он оставляет за бортом 11 человек из 20, то есть 55% — большую часть соискателей). А вот в ситуации дефицита кадров (когда на испытательный срок важно пригласить побольше людей), нам более полезен тест отбора (тест по истории позволяет допустить большую часть к испытательному сроку — 12 из 20, то есть 60%).

Оговорка. Впрочем, в данном случае понятия «тест отбора» и «тест отсева» — это лишь условные, взаимоотносительные понятия, которые можно поменять местами, если двигать вверх-вниз точки отсечения (cur score) на каждой оси каждого теста, а также если посчитать, что тестом отсева лучше называть такой тест, когда отсеивается меньшая часть, а тестом отбора — когда отбирается меньшая часть от общего числа соискателей. Но все-таки лучше называть тестом отсева именно такой тест, когда именно решение об отсеве порождает меньше вероятность ошибки, а не наоборот.

КОЭФФИЦИЕНТ ДИСКРИМИНАТИВНОСТИ — ЭТО НЕ ПАНАЦИЯ (!)

Интересно, заметить, что КД (коэффициент дискриминативности) в наших двух примерах у нас получился более высоким для теста по русскому языку, чем для теста по истории. Не буду приводить его простейшую формулу в этой статье (ну заманиваю я на нашу школу Вас, да — заманиваю), то привожу просто значения для двух ЧТС. Казалось бы всегда лучше применять тест, по которому получено более высокое значение КД. Ведь КД является интегральной мерой эмпирической валидности в данном случае! Но… как мы видим, если нам нужно из практических соображений больше людей привлечь к испытательному сроку, то лучше будет работать тест по истории, у которого даже более низкое значение КД, чем тест по русскому (!). — Это нетривиальное следствие мы получаем, разглядывая самые простейшие четырехклеточные таблицы.

РЕЗЮМЕ

В этой короткой статье я постарался предложить Вам, дорогие читатели, максимально наглядный пример двух таких таблиц ЧТС, которые бы позволили осознать, что такое валидность теста: это предсказательная способность, позволяющая по его результатам отнести человека к высокой или низкой группе по эффективности работы. С помощью ЧТС мы рассчитываем количественным образом плотность (силу) связи между результатами по тесту и гипотетическими показателями эффективности. Вот почему надо постараться понять, как ЧТС связана с корреляционным полем!

Мы предлагаем в нашей школе нашим слушателям интерактивную модель, позволяющую «подвигать мышкой» — поперемещать изображающие точки в корреляционном поле и сразу видеть, как меняется ЧТС и соответствующий коэффициент КД.

Обратите внимание заодно, откуда возникают ошибки понимания, глядя на приведенные здесь примеры с черными и белыми «шапочками». Одна из причин — это неспособность осмыслить разницу в буквенном обозначении клеточек ЧТС и цифровом обозначении квадрантов декартовой системы координат. Давайте-ка вспомним, как нумеруются квадранты в декартовой системе (координатные углы)? — Против часовой, начиная с верхнего правого угла! А как обозначаются клетки ЧТС? — Буквами по правилам чтения (по строкам слева направо, а затем сверху вниз), то есть это вовсе не против часовой, а другой принцип буквенного обозначения. Вот это несоответствие способов отображения мы стараемся помочь преодолеть в нашем практикуме. Казалось бы какой пустяк, да? — Но именно такие мелкие «детальки» очень часто мешают пониманию. Поэтому мы получаем на одну, а множество разных ЧТС в нашем практикуме и упражняемся вместе в их интерпретации (!).
Хотите этому поучиться? Хотите научиться строить свои собственные ЧТС для своих тестов и тестовых заданий? — Тогда записывайте в нашу зимнюю школу на следующей странице нашего сайта:

https://ht-line.ru/ktz-w

P.S.
Между прочим, я никак не прокомментировал в этой статейке, почему на рисунках корреляционного поля оси расположены с наклоном, а не обычным способом (перпендикулярная нижней кромки экрана ось Y и параллельная — ось X). Пусть это станет для Вас легкой загадкой, зачем я так сделал (?!). Кто догадается, дайте, пожалуйста, свой ответ в комментарии. ОК?