Уважаемые коллеги,

21 января запись в нашу виртуальную школу остановлена. Почему? — Потому что зарегистрировались уже 74 человека, из которых 37 начали активную работу. На внутреннем блоге-форуме школы после первой недели появилось уже более 100 сообщений (!).

Так что… если кто не успел, но интересуется, пожалуйста, подождите объявления о следующих циклах подобных «школ». Может быть, и «летняя» такая случится.

Ваш АШ

======================================

Здравствуйте, коллеги!
Еще раз всех с наступившим НГ-2019.

ПРОСЬБА: пожалуйста, поставьте этому сообщению лайк, если Вы считаете, что такую тематику нужно развивать СИСТЕМАТИЧЕСКИ — в рамках некой виртуальной «зимней психометрической школы».

СВОДКА: после 1-го дня лайки поставили 14 человек. Если учесть, что половине из них такой ликбез НЕ нужен, то это маловато, конечно.
Коллеги, если у кого-то будет возможность пригласить каких-то знакомых эйчаров (или психологов), то это будет хорошо. Мне пока не дают анонсировать такие мероприятия в группах для эйчаров (как правило, не дают).

Сейчас в эпоху повального увлечения мощными ГОТОВЫМИ инструментами анализа данных возникает опасность еще большего разрыва между Специалистами и специалистами (одни пишутся с заглавной буквы, другие со строчной), между Аналитиками и пользователями (другими словами о том же). Разрыва в понимании СМЫСЛА АНАЛИТИЧЕСКИХ ПРОЦЕДУР.

Даже базовые представления о корреляции в силу легкости подсчета показателей корреляции СНИЖАЮТСЯ или даже… «улетучиваются». Я это видел своими глазами не раз, когда просил «пользователей-специалистов» просто правильно разместить данные в электронной таблице — так, чтобы можно было их проанализировать с помощью коэффициента корреляции. НЕ МОГУТ (!?!).

В связи с этим давайте попробуем еще раз поискать подходящий формат общения на эти темы. Прошлой попыткой стали «виртуальные психометрические ужины» — одномоментные вечерние онлайн-конференции в формате «чата». Выражали к ним интерес многие, но мало кто находил время вечером (в 21.00), а еще раньше — еще меньше 

Теперь вот думаю… Думаю о том, не попробовать ли банальные видео-лекции? — На самые банальные темы вроде «четырехклеточной корреляции», которую, увы, по моим представлениям многие «пользователи» до сих пор не освоили. Польза от видеолекций в том, что их можно смотреть асинхронно и… задавать вопросы. Причем, чтобы откладывание просмотра не превращалось в дурную бесконечность, думаю, что надо ограничить гарантированное время ответов на вопросы — например, одна неделя и не больше.

Но… громоздить видео-лекцию на ту или иную тему — это опять-таки определенный труд. Для меня это труд бОльший, чем анонсировать эту тему в письменном виде. Вначале надо бы получить на анонс какой-то отклике, а затем уже — громоздить видео-лекцию в уверенности, что аудитория будет достаточно большой, что это труд имеет смысл…

Итак, про четырехклеточные таблицы сопряженности (ЧТС).
Краткий план видео-лекции рождается примерно таким:

1) Качественные данные и пересекающиеся множества (на диаграммах Венна).
2) Построение ЧТС на основе диаграммы Венна (для «пересекающихся кругов»).
3) Декартова система координат и ЧТС.
4) Конфигурация эллипсоида рассеяния в декартовой системе координат и ЧТС.
5) Логические таблицы истинности и ЧТС
6) Подсчет коэффициентов дискриминативности (КД) по строкам и столбцам ЧТС.
7) Почему КД имеет разные значения по строкам и столбцам?
8) Плюсы и минусы простейшего КД.
9) Примеры подсчета КД для анализа «внешней валидности теста по критерию».
10) Чем Фи-коэффициент удобней и полезней по сравнению с КД?
11) Оценка значимости Фи-коэффициента.
12) Построение ЧТС с помощью расщепления по медиане.
13) Построение ЧТС по крайним (экстремальным) группам — по терцилям и квартилям.
14) Как связаны КД, Фи и Линкор (линейная корреляция Пирсона) на одном массиве данных?

Итак, покажем ниже фрагмент такой видео-лекции. Причем начнем… с конца — осветим пункт 14.

Только что мы опубликовали здесь на форуме (и в группе TESTbyTEST на ФБ) данные о том, как связан возраст с успешностью в новогодней тест-игре MidiMelody. Напомним еще раз, как выглядит таблица и соответствующая диаграмма:

Конкурные Баллы	Молодые (до 33)	Старшие (от 34)
0- 300	46%	25%
301- 700	30%	23%
701- 1100	16%	28%
1101 -1500	8%	25%

А вот соответствующая диаграмма:

Таблица, которая дается выше, НЕ ЯВЛЯЕТСЯ таблицей вида ЧТС по двум признакам:

1) Количество строк больше двух.
2) В клеточка даются проценты, а не частоты (численность испытуемых).

Для начала вернемся к частотам:

Конкурс. баллы	Молодые	Старшие
0- 300	35	20
301- 700	23	18
701- 1100	12	22
1101 -1500	6	20

Поясним, что в левой верхней клетке число 35 указывает на число
молодых людей, которые попали в самый низкий интервал по величине
конкурсного балла.

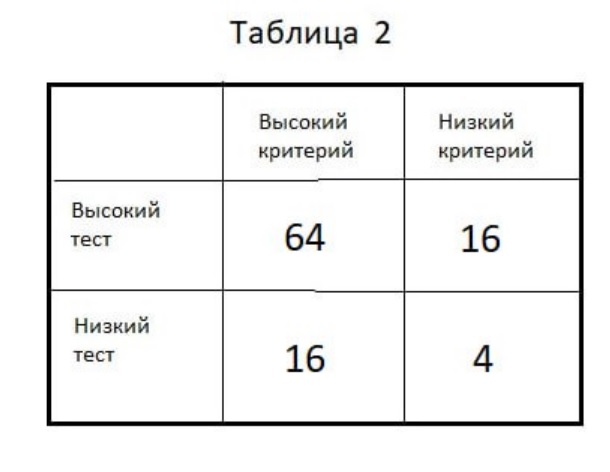
А вот как выглядит ЧТС, построенная на базе указанной восьмиклеточной таблицы:

Расщепление по медиане
Тест\Критерий	До 33	После 33
Низкая Группа	58	38
Высокая группа	18	42
КД=	0,76	0,48	0,28

Поясним, как подсчитан ПРОСТЕЙШИЙ коэффициент дискриминативности (КД) по этой ЧТС. Это можно сделать буквально «на пальцах».

1) Шаг 1: считаем 0,76 — это отношение численности успешных к общей численности в группе молодых (58/76 = 0,76).
2) Шаг 2: считаем 0,48 — — это отношение численности успешных к общей численности в группе старших (38/80 = 0,48).
3) Шаг 3: считаем разность этих двух дробей и получаем КД=0,28.

Вопрос: 0,29 — это много или мало? Это значимо или можно пренебречь?

Напомним, что соответствующий линейный коэффициент Пирсона (Линкор) равен 0,37,
что обладает очень высокой значимостью (на уровне ошибки p<0,001 при численности выборки n=156).

А теперь ГЛАВНЫЙ ВОПРОС (для этой части номер 14 лекции):

Почему КД оказался ниже, чем Линкор? — Почему 0,28, а не 0, 37?

Итак, стоит прежде всего обратить внимание, что ЧТС, указанная выше, получена путем самого грубого расщепления — по медиане. Клеточки этой ЧТС получены путем суммирования клеточек восьмиклеточной таблицы, так что в «низкую группу по конкурсному баллу» попали те испытуемые, которые набрали 700 очков и меньше, а в «высокую группу» — те, кто набрали больше 700 очков. При медианном расщеплении испытуемые, которых отделяет друг от друга только 1 очко (тот, у кого 701 попадает уже в высокую группу, а у кого 700 — в низкую), на самом деле могут по своим результатам НЕ РАЗЛИЧАТЬСЯ ЗНАЧИМО. Чтобы взять заведомо более значимые различия, давайте произведем анализ по «крайним» группам — произведем расщепление по четвертям (примерным четвертям). Тогда ЧТС будет выглядеть так:

Расщепление по квартилям
Тест\Критерий	До 33	После 33
Низкая	35	20
Высокая	6	20
КД1=	0,85	0,50	0,35

Как видим, в данном случае КД уже приближается к значению Линкор (0,37), но… все-таки его не достигает.

Но… КД может оказаться для этой же самой ЧТС и выше, если просто «перевернуть» (точнее транспонировать) таблицу — поменять местами строки и столбцы:

Критерий\Тест	Низкая	Высокая
До 33	35	6
После 33	20	20
КД2=	0,64	0,23	0,41

Ого! — Получили даже более высокое значение, чем Линкор, а именно — 0,41.
Оказывается, КД меняется в зависимости от того, как мы считаем дроби
— по строкам или по столбцам. Мы видим это на данном примере ярко!
А вот среднее арифметическое значение КД1 и КД2 равно 0,38.
Оно уже неплохо приблизилось к Линкор (0,37).

Вставка: тут меня спросили: А зачем транспонировать? Мой ответ: эта
операция показывает, что некоторые коэффициенты меняются, если
поменять местами строки и столбцы. А мы ведь ожидаем, что ничего
не меняется «от перемены мест слагаемых», а это, увы, не «слагаемые»
вовсе. И не все коэффициенты получают одно и то же значения.

Неужели КД надо каждый раз считать дважды? — Увы, чтобы не обмануться
надо! Причем чем больше асимметричными оказываются переменные по строкам
и столбцам (краевые суммы не равны), тем в большей степени этот двойной подсчет необходим (!).

А что нам дает подсчет для этой ЧТС фи-коэффициента? Оказывается Фи-корреляция Гилфорда равна 0,38, причем значение это НЕ зависит от того, какую таблицу мы берем (исходную или транспонированную), ибо коэффициент Фи не зависит от того, что по строкам и что по столбцам. Видим, что его значение совпадает с усредненным КД (0,38) и сразу же неплохо приближается к Линкор (к 0,37).

Значимость Фи-коэффициента легко оценить по следующей формуле, являющейся обратным преобразованием статистического критерия Хи-квадрат
для уровня значимости p<0,001 и одной степени свободы:

ФИкрит = КОРЕНЬ(10.8/(35+6+20+20) = 0,365

Уфф! Значимость того же высокого уровня (низкой вероятности ошибки) с помощью ФИ достигнута (того, что и для линейной корреляции), но… едва-едва. Так что на этом примере видим, что проверка значимости Фи-коэффициента ведет себя даже строже (!).

ИТАК. ОБЩИЙ ВЫВОД.

Произведенные «на пальцах» расчеты на указанном понятном (я надеюсь!) примере иллюстрируют для нас смысл Фи-коэффициента как наиболее удобного инструмента для измерения статистической связи двух бинарных переменных, связанных друг с другом с помощью ЧТС — четырехклеточной таблицы сопряженности. Эти расчеты показывают, что при достаточно сбалансированных двух переменных значения Фи-коэффициента оказывается весьма близким к значению линейной корреляции. Но… на мой вкус, все, что нам дает ЧТС по сравнению с линейной корреляции — это гораздо более высокая наглядность полученной связи: пропорция в одной группе ИНАЯ, чем в другой (!) — в этом смысл, это надо постараться ПОНЯТЬ. Как? — Ну хотя бы просто раскрыть глаза и увидеть, глядя на значения частот в «четырех соснах» — в четырех клеточках таблицы.

ЛИРИЧЕСКОЕ ОТСТУПЛЕНИЕ: про строки, столбцы и конкретное мышление.

Что такое конкретное мышление? — Абстрактное понятие связано намертво с определенной «наглядной картинкой». Например, чтобы увидеть прямой угол в треугольнике, этот треугольник для человека с конкретным, наглядно-образным мышлением приходится обязательно размещать так, чтобы он «стоял на одном из катетов», а прямой угол находился обязательно сбоку. А если такой прямоугольный треугольник положить на гипотезу, так что прямой угол окажется верхним, то… конкретное мышление может вовсе не опознать, что этот треугольник является прямоугольным (?!). Почему? — А ему легче «разглядеть» прямой угол, когда одна линия идет строго по горизонтали (один катет), а другая -строго по вертикали (другой катет).

Примерно тоже самое получается у нас с пресловутыми этими ЧТС — четырехклеточными таблицами. Стоит произвести транспонирование и… перестает распознаваться такая структура данных, которая работает на проверку валидности. Ибо человек с конкретным мышлением должен обязательно привыкнуть «ВИДЕТЬ», что по столбцам — критерий, а по строкам — результаты теста (попадание в высокую и низкую группу), а если по-другому… то, ситуация уже не распознается. Я это видел СОТНИ РАЗ у студентов психологов старше 20 лет. Студентов МГУ (!), а что Вы хотите от рядовых эйчаров, которым, как и кассирам-операционистам, ни одну формулу нельзя давать в руки, а надо давать «таблицы перевода» (сырых баллов в стандартные, например), ибо таблицами они пользоваться умеют, а формулами… нет.

О том, как трудно усваивать абстрактные математические правила, говорит нам опыт преподавания математики для … маленьких детей (до 9-10 лет, когда логичекое мышление только-только вызревает). Правила математики у детей срастаются с образами конкретных предметов. И это на данном этапе не так плохо! Нужно этим пользоваться, чтобы ребенок мог хотя бы в конкретной форме что-то освоить. А если у него в голове мелькают и «толкаются» разные картинки, то он будет обязательно путаться. Например, если раньше времени ребенку начать ВБИВАТЬ коммутативный закон умножения (от перемены мест сомножителей произведение не меняется), то он… начинает путаться в делении, ибо НЕ ПОНИМАЕТ, какой именно делитель надо выбрать для решения той или иной содержательной задачи. Но… об этом в другой ветке идет разговор — «Сколько яблок растет на березе».